Multistep Reasoning Agents (with GRPO & RLEF) - Project Euler Edition

Published: at 02:38 AM in 21 min readSuggest Changes

Transforming LLMs into Mathematical Problem Solvers: How GRPO with execution feedback creates reasoning agents that tackle Project Euler’s algorithmic challenges through multi-step reasoning and efficient code generation.

Table of Contents

Open Table of Contents

Introduction

In the rapidly evolving landscape of AI, we’ve seen remarkable progress across several “types” of models:

However, models that seamlessly combine all these capabilities remain elusive, with truly effective AI agents representing perhaps the most significant challenge.

Among these frontiers, the development of AI systems that can act with agency while leveraging sophisticated reasoning and tool use stands prominently as the upcoming problem to solve. The ability to break down complex tasks, formulate plans, verify intermediate results, and adapt strategies based on feedback—all while maintaining coherent reasoning—requires an integration of capabilities that existing models struggle to achieve consistently.

By combining Group Relative Policy Optimization (GRPO) with Reinforcement Learning from Execution Feedback (RLEF), we make progress towards a system that doesn’t just memorize solutions but learns to reason through problems, execute code iteratively, and refine its approach based on runtime feedback. Applied to the challenging Project Euler dataset, our method achieves a significant improvement on both training problems and on unseen test problems, with dramatic reductions in execution time and memory usage.

What makes our approach unique is its ability to convert general-purpose chat models into specialized reasoning agents without architecture changes—simply through reinforcement learning with carefully designed reward functions that emphasize both correctness and efficiency. The results demonstrate how execution-based feedback can bridge the gap between academic benchmarks and practical algorithmic problem-solving capabilities that programmers need in real-world scenarios.

If you are interested in running experiments on your own, you can find the code and instructions on my fork of verifiers. Underneath the hood, verifiers uses:

Project Euler

Project Euler [1] is a series of challenging mathematical and computational problems designed to be solved with computer programs. Named after the Swiss mathematician Leonhard Euler (1707-1783), the project was launched in 2001 by Colin Hughes and has since grown to contain over 800 problems of varying difficulty.

What makes Project Euler particularly suitable for testing AI reasoning capabilities:

  1. Clear success criteria: Each problem has a single, definitive numerical answer that can be verified.
  2. Reasoning chain requirement: Solutions typically involve multiple steps of reasoning and cannot be solved through memorization.
  3. Algorithm efficiency matters: Many problems can be approached with naive algorithms that would take years to complete, forcing the development of more elegant solutions.
  4. Mathematical knowledge application: Solving problems requires applying concepts from number theory, combinatorics, probability, and other mathematical domains.
  5. Increasing difficulty curve: Problems range from accessible to extremely challenging, providing a natural progression for testing AI capabilities.

In our GRPO (Group Relative Policy Optimization) experiments, we use Project Euler problems as an ideal testbed because they require both code generation and mathematical reasoning. The clear verification signal (correct/incorrect answer) provides an unambiguous reward function for our reinforcement learning approach. Measuring runtime performance provides a natural reward signal that encourages efficient solutions.

Downloading Dataset from Huggingface Hub

from datasets import load_dataset

# Load the entire dataset with all splits
dataset = load_dataset("alexandonian/project-euler")

# Work with specific splits
train_problems = dataset["train"]
hard_problems = dataset["hard"]
sample_problems = dataset["sample"]

# Example: Get a problem
problem = train_problems[0]
print(f"Problem #{problem["id"]}: {problem["title"]}")
print(problem["problem"])
print(f"Answer: {problem["numerical_answer"]}")

# Example usage:
# First problem from the 'train' split:
# Problem #768: Chandelier
# Difficulty: 95%
# Problem:
# -------
# A certain type of chandelier contains a circular ring of $n$ evenly spaced candleholders.
# If only one candle is fitted, then the chandelier will be imbalanced. However, if a second
# identical candle is placed in the opposite candleholder (assuming $n$ is even) then perfect
# balance will be achieved and the chandelier will hang level.

# Let $f(n,m)$ be the number of ways of arranging $m$ identical candles in distinct sockets of a
# chandelier with $n$ candleholders such that the chandelier is perfectly balanced.

# For example, $f(4, 2) = 2$: assuming the chandelier's four candleholders are aligned with the
# compass points, the two valid arrangements are "North & South" and "East & West". Note that these
# are considered to be different arrangements even though they are related by rotation.

# You are given that $f(12,4) = 15$ and $f(36, 6) = 876$.
# Find $f(360, 20)$.

# Answer: 14655308696436060

GRPO

GRPO was first introduced in the DeepSeek-R1 [2] release, which made serious waves in the community when it was first announced in January of 2025. The waves were large enough to move the stock market!

GRPO Workflow

At high level, GRPO requires the following components:

GRPO consists of the following steps:

  1. For each input prompt pp, sample a group of NN responses G={r1,r2,…,rN}\mathcal{G} = \{r_1, r_2, \ldots, r_N\} from the current policy πθ\pi_{\theta}.
  2. Compute the reward R(ri)R(r_i) for each response rir_i in the group G\mathcal{G}.
  3. Calculate group-normalized advantage for each response: Ai=R(ri)−mean(G)std(G)A_i = \frac{R(r_i) - \text{mean}(\mathcal{G})}{\text{std}(\mathcal{G})}

Then the GRPO objective is the following:

Lclip(θ)=1N∑i=1N(min⁡(πθ(ri∣p)πθold(ri∣p)Ai, clip(πθ(ri∣p)πθold(ri∣p),1−ϵ,1+ϵ)Ai)),\mathcal{L}_{\text{clip}}(\theta) = \frac{1}{N}\sum_{i=1}^{N}\left(\min\left(\frac{\pi_\theta(r_i|p)}{\pi_{\theta_{\text{old}}}(r_i|p)}A_i, \text{ clip}\left(\frac{\pi_\theta(r_i|p)}{\pi_{\theta_{\text{old}}}(r_i|p)}, 1-\epsilon, 1+\epsilon\right)A_i\right)\right),

then with the KL penalty term, the final GRPO objective can be written as:

LGRPO(θ)=Lclip(θ)⏟Maximize reward−w1DKL(πθ∣∣πorig)⏟Penalize KL divergence\mathcal{L}_{\text{GRPO}}(\theta) = \underbrace{\mathcal{L}_{\text{clip}}(\theta)}_{\text{Maximize reward}} - w_1 \underbrace{\mathbb{D}{\text{KL}}\left(\pi_\theta||\pi_{\text{orig}}\right)}_{\text{Penalize KL divergence}}

Reinforcement from Execution Feedback (RLEF)

Reinforcement Learning from Execution Feedback (RLEF) is a technique where AI models learn to generate better code by receiving feedback from actual execution results. Unlike traditional supervised learning approaches, RLEF doesn’t require labeled examples of “good” code but instead relies on whether the generated code runs correctly and efficiently.

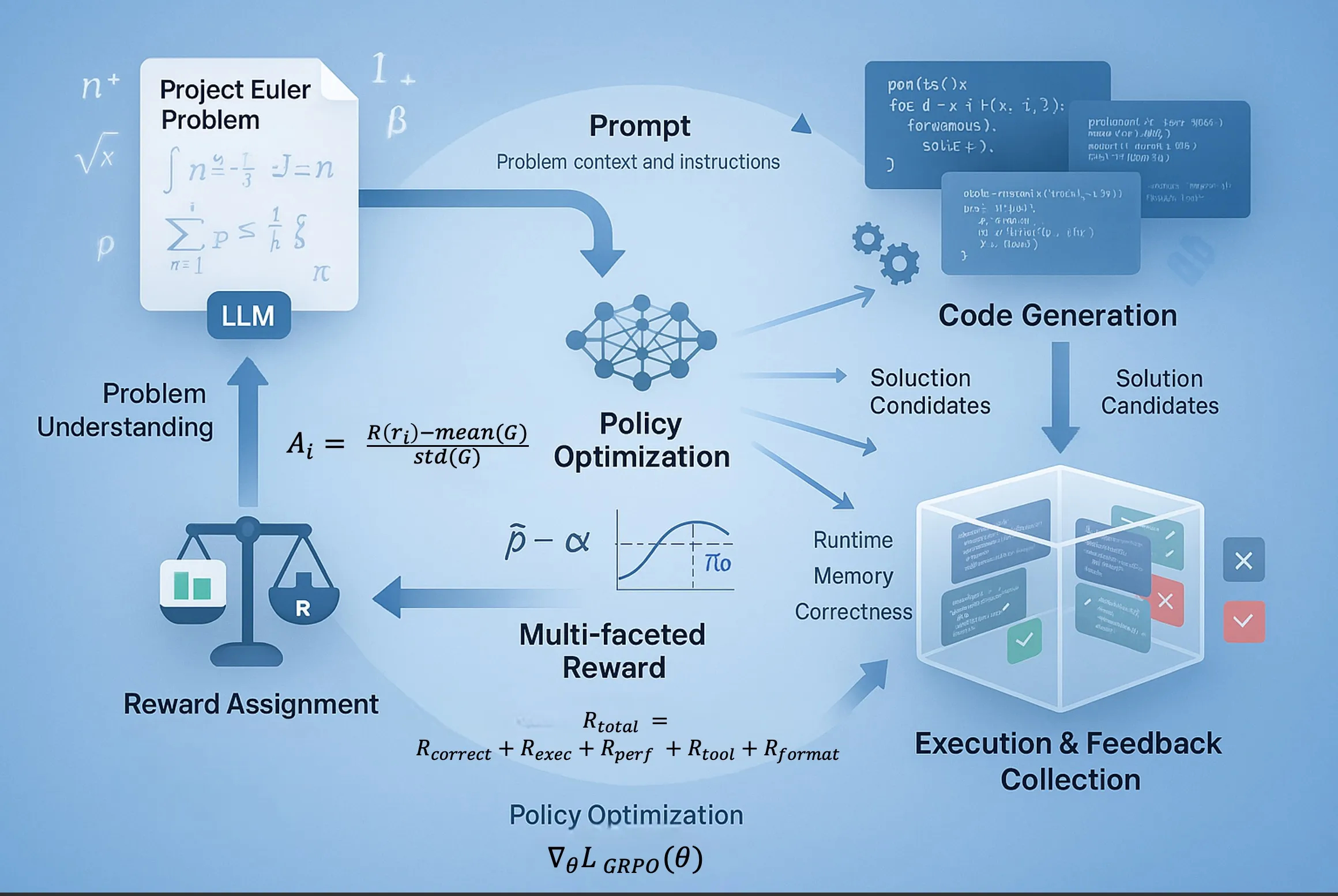
Swirling-thoughts

Reinforcement Learning from Execution Feedback (RLEF) process for Project Euler problems. The LLM policy model generates multiple solution candidates for each problem. These candidates are executed in a sandboxed environment, which produces performance metrics including correctness, runtime efficiency, and memory usage. These metrics are transformed into a scalar reward through our multi-component reward function. The GRPO algorithm then uses these rewards to update the policy model, prioritizing solutions that are both correct and efficient while maintaining proximity to the reference model. This closed feedback loop enables the model to progressively learn elegant algorithmic approaches rather than brute-force solutions.

In our Project Euler context, RLEF works as follows:

  1. Generation: The LLM generates Python code to solve a given Project Euler problem.
  2. Execution: The code is executed in a (mostly) controlled environment.
  3. Feedback Collection: We collect various signals from the execution:
    • Did the code run without errors?
    • Does it produce the correct answer?
    • How long did it take to execute and how much memory did it use?
    • Did the model format its reasoning, requests for code execution/tools, and final answer correctly?
  4. Reward Calculation: These signals are converted into a scalar reward.
  5. Policy Update: The LLM is updated using GRPO to maximize this reward.

This approach is particularly powerful for code generation because:

For Project Euler problems, execution feedback is especially valuable as many problems have naive solutions that are correct but computationally intractable, forcing the model to learn more sophisticated algorithms.

Rewards:

Our RLEF approach uses a comprehensive set of reward functions to guide the model’s learning process. These rewards are carefully designed to promote not just correct answers, but efficient, well-structured code and effective use of available tools.

Detailed Reward Functions

Our reward system incorporates multiple components that evaluate different aspects of the model’s performance:

  1. Correctness Rewards:

    • correct_answer_reward_func: The primary reward that evaluates if the final solution matches the expected answer (1.0 for correct, 0.0 for incorrect)
    • mc_reward_func, math_reward_func, code_reward_func: Task-specific correctness evaluation for multiple-choice, mathematical expressions, and code generation

  2. Code Execution Rewards:

    • code_execution_reward_func: Rewards successful code execution without errors (weighted at 0.5)
    • code_performance_reward_func: Evaluates runtime efficiency and memory usage (weighted at 0.25)

  3. Tool Usage Rewards:

    • tool_execution_reward_func: Rewards successful tool calls (weighted at 0.5)
    • Tool-specific rewards that track usage patterns of individual tools

  4. Format Adherence Rewards:

    • format_reward_func: Ensures proper formatting of reasoning, code, and answer sections
    • xml_reward_func: Verifies correct XML structure throughout the response

The reward function dynamically adapts to the execution environment, with performance metrics normalized within each solution group to handle the variability in problem difficulty.

The formula that combines these individual rewards is:

Rtotal=wcorrect⋅Rcorrect+wexec⋅Rexec+wperf⋅Rperf+wtool⋅Rtool+wformat⋅RformatR_{total} = w_{correct} \cdot R_{correct} + w_{exec} \cdot R_{exec} + w_{perf} \cdot R_{perf} + w_{tool} \cdot R_{tool} + w_{format} \cdot R_{format}

Where:

This multi-faceted reward approach encourages the model to develop solutions that are not only correct but also efficient, well-structured, and make appropriate use of available tools.

Key Innovations of Our Approach

Our implementation brings several unique advantages that differentiate it from other RL-based code generation systems:

Conversion of Chat Models into Reasoning Agents

Unlike approaches that start with specialized code models, we transform a general-purpose chat model (Qwen2.5-7B-Instruct) into a powerful reasoning agent. This demonstrates how RLEF can enhance existing models without requiring specialized architectures, making the approach more accessible and adaptable.

Multi-step Mathematical Reasoning with Environment Feedback

Our training process emphasizes structured mathematical reasoning within an interactive feedback loop, enabling and encouraging the agent to discover and implement more elegant algorithmic solutions rather than brute-force approaches. The model is trained to:

  1. Break down problems into manageable mathematical components, discussing its approach in opening <reasoning></reasoning> tags
  2. Verify intermediate calculations using the calculator tool or code execution.
  3. Receive feedback from the execution environment, including error messages, warnings, and performance metrics.
  4. Incorporate this feedback to revise its approach, retrying if necessary before translating the output into a final solution formatted in <answer></answer> tags.

This natural multi-turn interaction creates a robust problem-solving process that mimics how human programmers debug and refine their solutions, with each step informing the next in a continuous improvement cycle that enhances the model’s understanding and assists users in achieving their objectives.

Native Code Execution Support with Correctness and Performance Rewards

Rather than forcing code into restrictive JSON formats, our implementation allows the model to write code in natural XML blocks:

<code>
def is_prime(n):
    if n <= 1:
        return False
    if n <= 3:
        return True
    if n % 2 == 0 or n % 3 == 0:
        return False
    i = 5
    while i * i <= n:
        if n % i == 0 or n % (i + 2) == 0:
            return False
        i += 6
    return True

print(is_prime(1000003))
</code>
<code_result execution_time="41" memory_used="3708000">
True
</code_result>

This approach preserves code readability and allows the model to express solutions in a more natural programming style, improving both training efficiency and the quality of generated solutions.

Experimental Setup

Model Architecture

We use the Qwen2.5-7B-Instruct as model as our base policy model, a strong language model with strong coding and mathematical reasoning capabilities. For our reference model, we use the original (non-fine-tuned) version of the same architecture to ensure compatibility in the KL divergence calculations.

Training Dataset

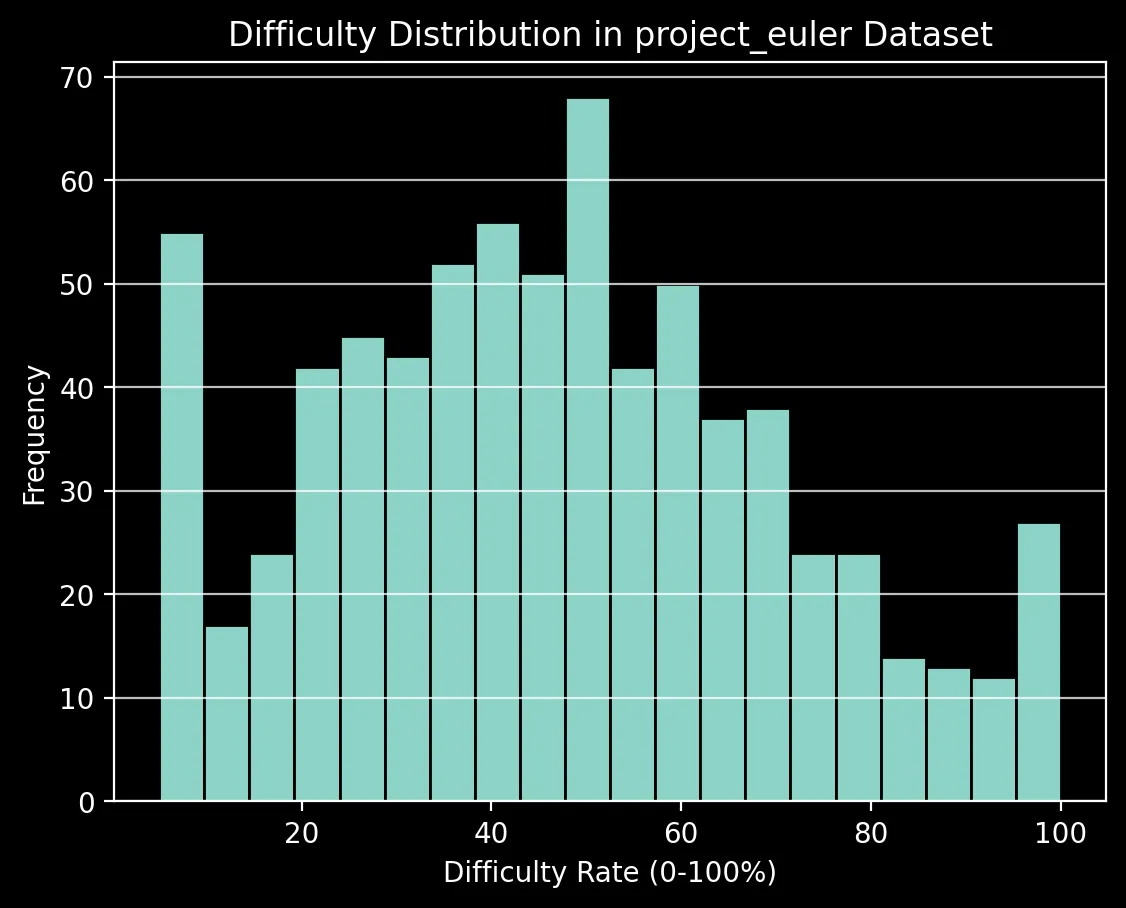
We selected 734 Project Euler problems ranging from difficulty levels providing a good distribution of problems that test various mathematical and algorithmic concepts.

Difficulty Distribution of Project Euler Problems

Prompt Engineering

System Prompt

Code+Tool Use System Prompt 
Use step-by-step reasoning, code execution and the following tools to help solve problems:

calculator: Evaluates a single line of Python math expression. No imports or variables allowed.

Arguments:
  - expression: A mathematical expression using only numbers and basic operators (+,-,*,/,**,())

Examples:
  "2 + 2" -> "4"
  "3 * (17 + 4)" -> "63"
  "100 / 5" -> "20.0"

Returns: The result of the calculation or an error message (str)

For each step:
1. Think through your reasoning inside <reasoning> tags
2a. If needed, use a tool by writing a JSON command inside <tool> tags with:
   - "name": the tool to use
   - "args": the arguments for the tool

Example usage:
<tool>
{"name": "calculator", "args": {"expression": "715.019337 / 4.0"}}
</tool>


2b. Write Python scripts inside <code> tags to work out calculations
   - Functions and variables do not persist across <code> calls and should be redefined each time
   - Scripts should be written in Python 3.10+ syntax, and should run in under 10 seconds
   - Any desired outputs should be printed using print() statements
   - You may import numpy, scipy, and sympy libraries for your calculations

Example usage:
<code>
import numpy as np
result = np.sqrt(16)
print(result)  # This will output 4.0
</code>

3a. You will see the tool's output inside <result> tags
3b. You will see the output from print() statements in your code in <code_result> tags
4. Continue until you can give the final answer inside <answer> tags

The <answer>...</answer> tags should contain only your final answer.

Example for multiple choice questions:
<answer>
A
</answer>

Example for math problems:
<answer>
\frac{1}{2}
</answer>

Tools expect specific JSON input formats. Follow the examples carefully.
Do not make up tools or arguments that aren't listed.

GRPO Configuration

Environment & Execution Environment

Code execution is performed in a sandboxed Python 3.12 environment with:

Results

After training with GRPO for RLEF, we observed significant improvements across multiple dimensions of performance:

Overall Accuracy Improvements

The GRPO-trained model demonstrated substantial gains in problem-solving capacity:

SplitBefore GRPOAfter 500 GRPO StepsImprovement
Train1.1% (3/184)7.4% (13/184)+573%
Test5.9% (11/184)9.2% (17/184)+57%

These figures represent an increase in the model’s ability to solve Project Euler problems correctly. The higher improvement rate on the training set suggests that the model has effectively learned from the reinforcement signal, while still generalizing to unseen problems as shown by the test set improvement.

Reward Component Analysis

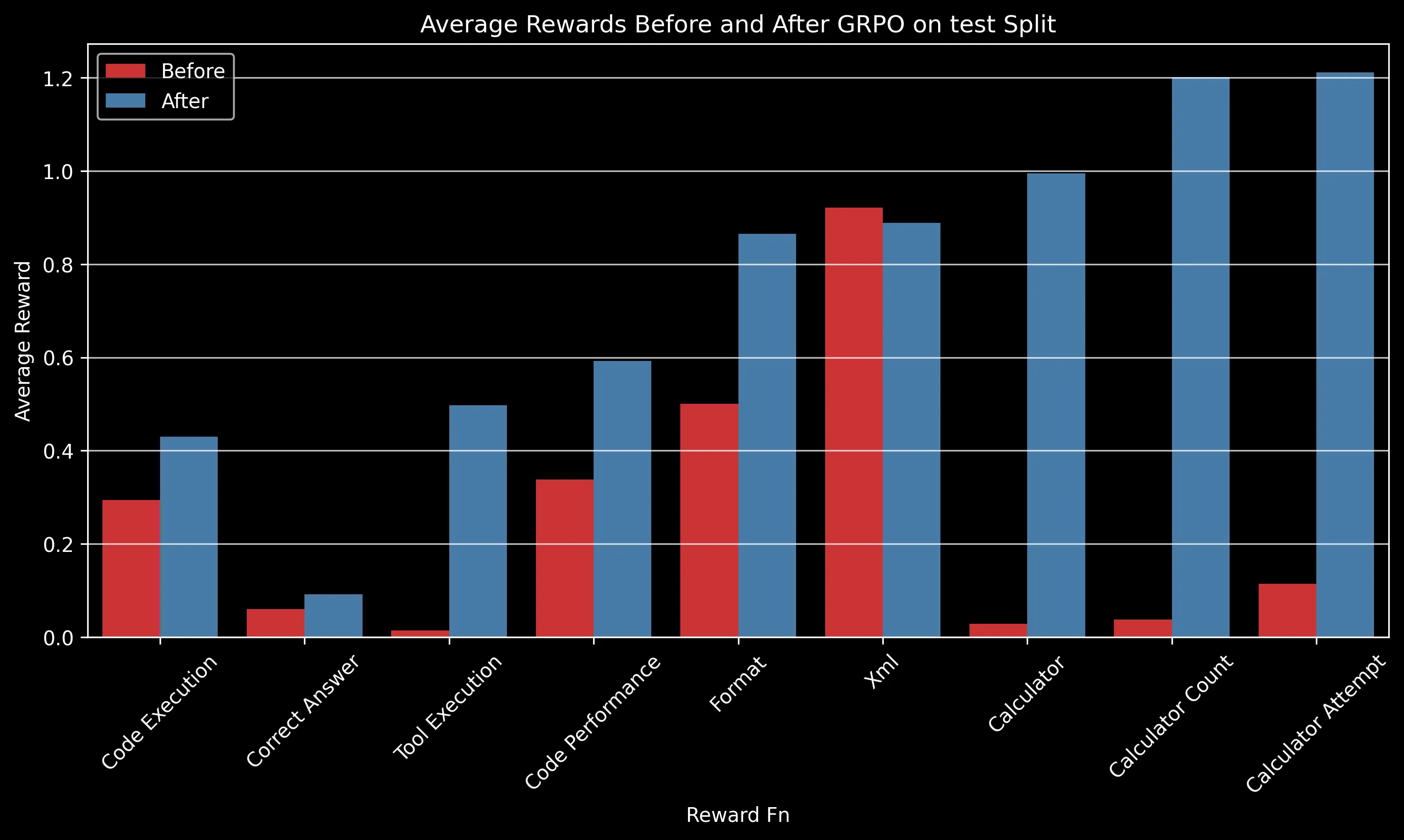
Average Rewards on Test Split

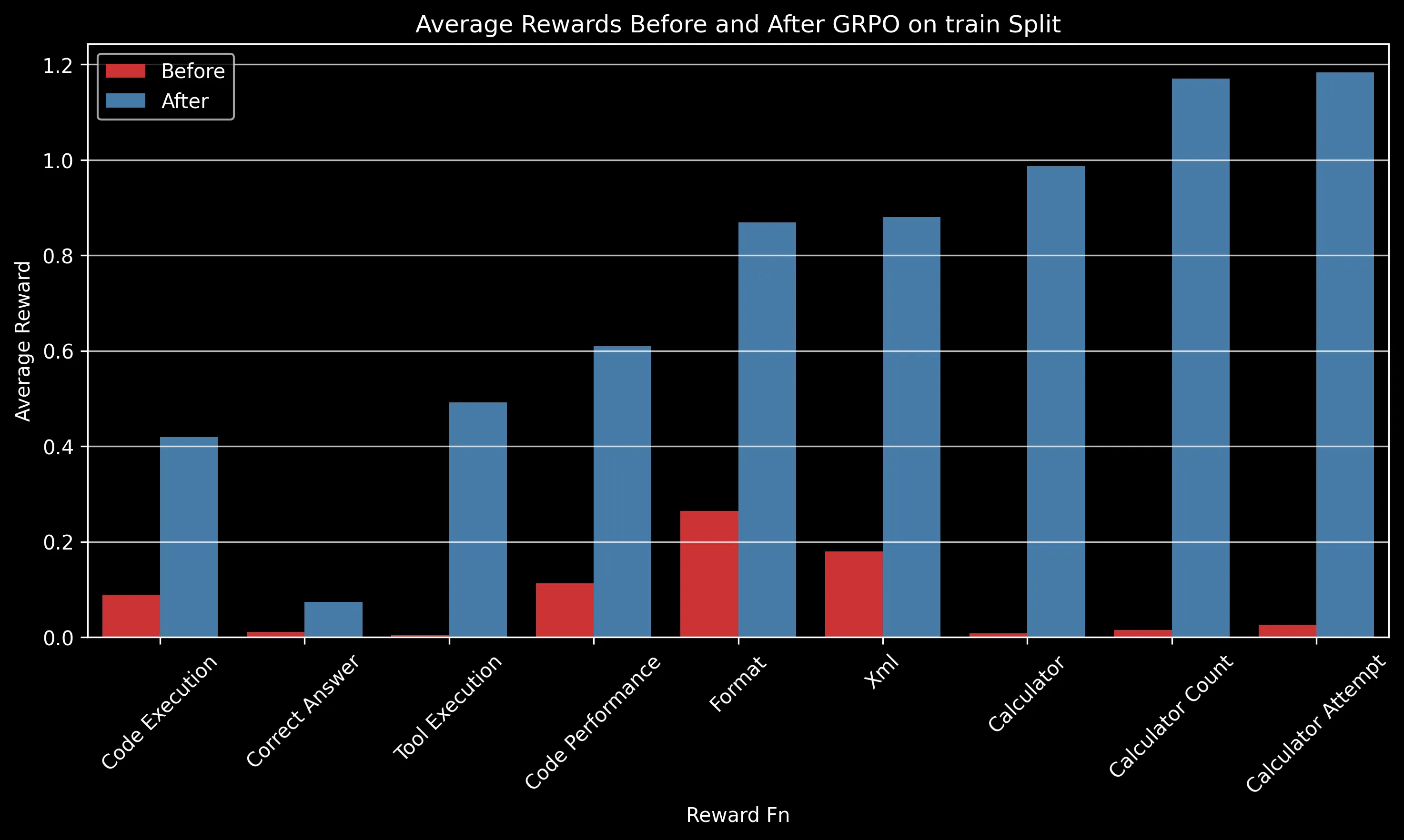
The charts above show how different reward components improved after GRPO training. Some key observations:

  1. Code Execution: Increased from ~0.3 to ~0.42 on the test split, indicating significantly fewer runtime errors
  2. Tool Execution: One of the most dramatic improvements, increasing from near 0 to ~0.5, showing the model learned to effectively use provided tools
  3. Calculator Usage: Perfect calculator usage (1.0) after training compared to minimal usage before
  4. Code Performance: Notable improvement from ~0.35 to ~0.6, reflecting more efficient code generation

Performance by Problem Difficulty

We analyzed how the model’s performance varies across different difficulty levels of Project Euler problems:

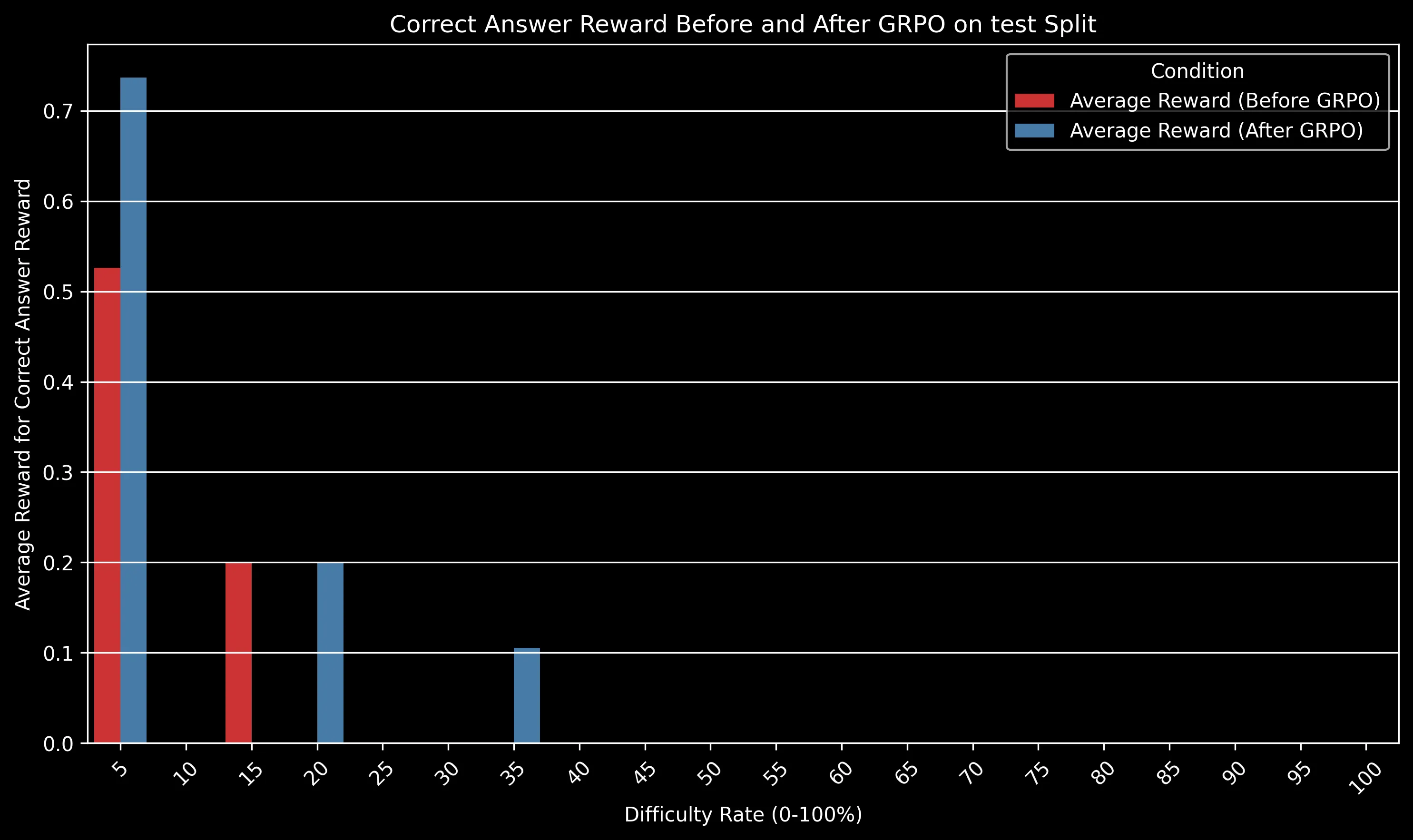
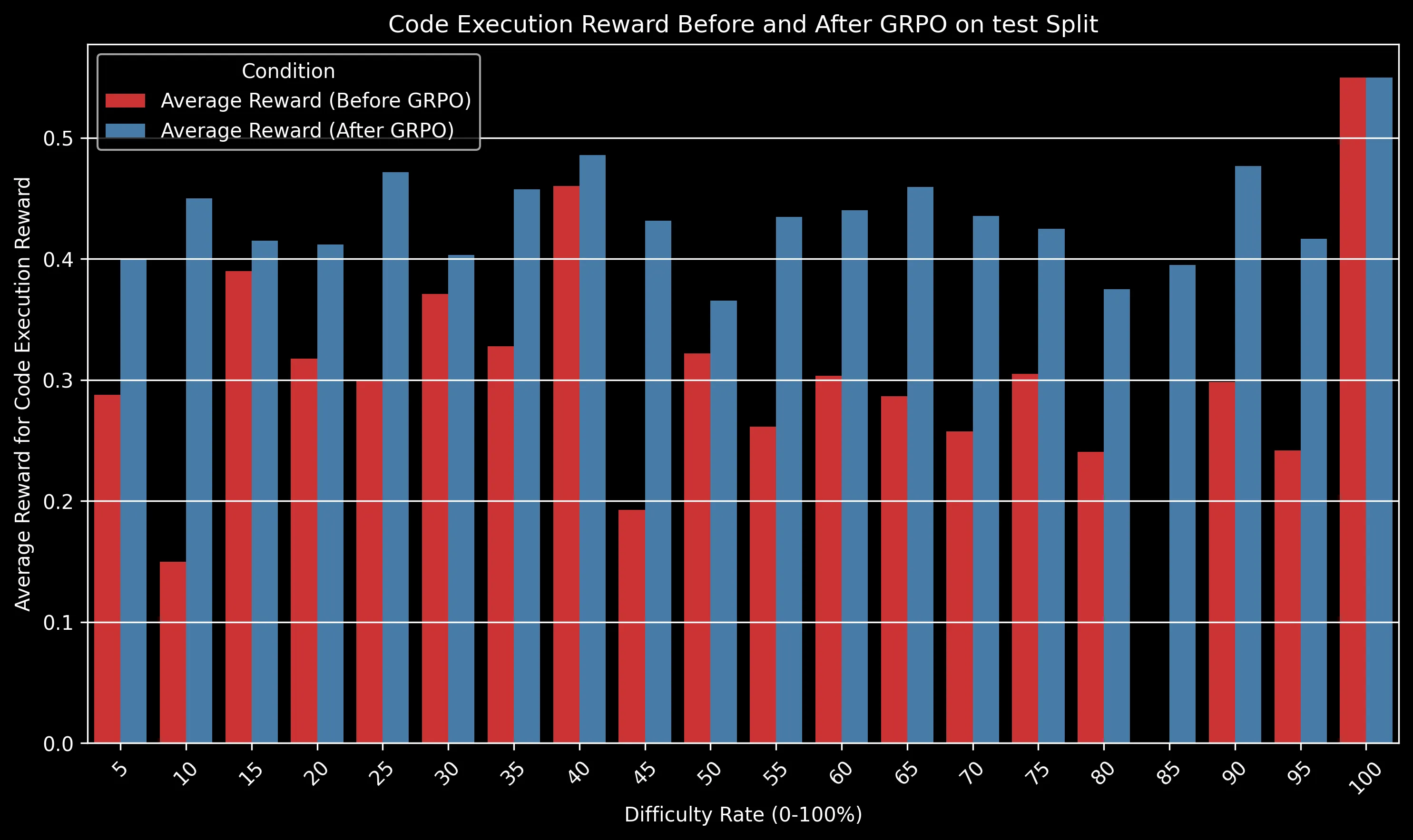
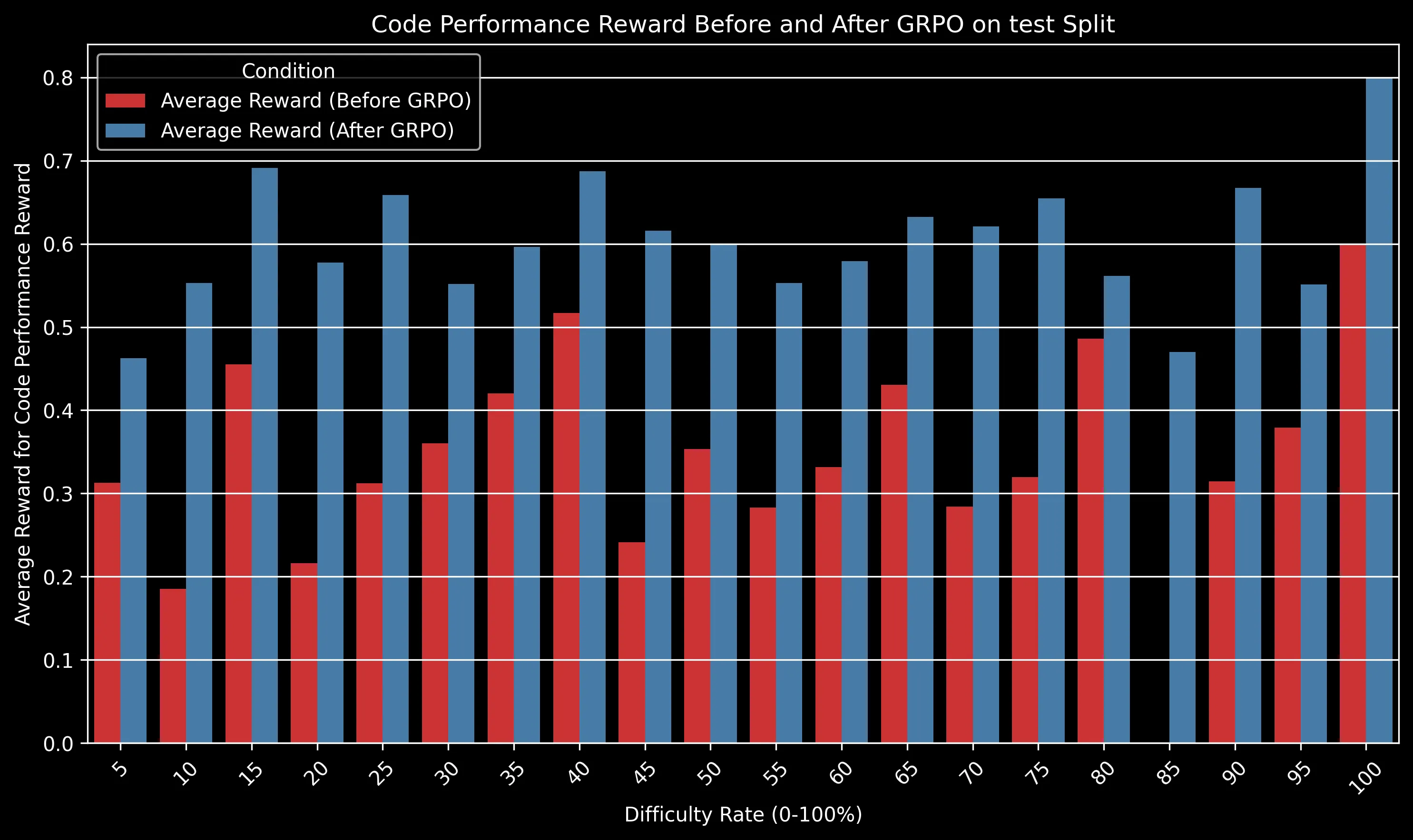
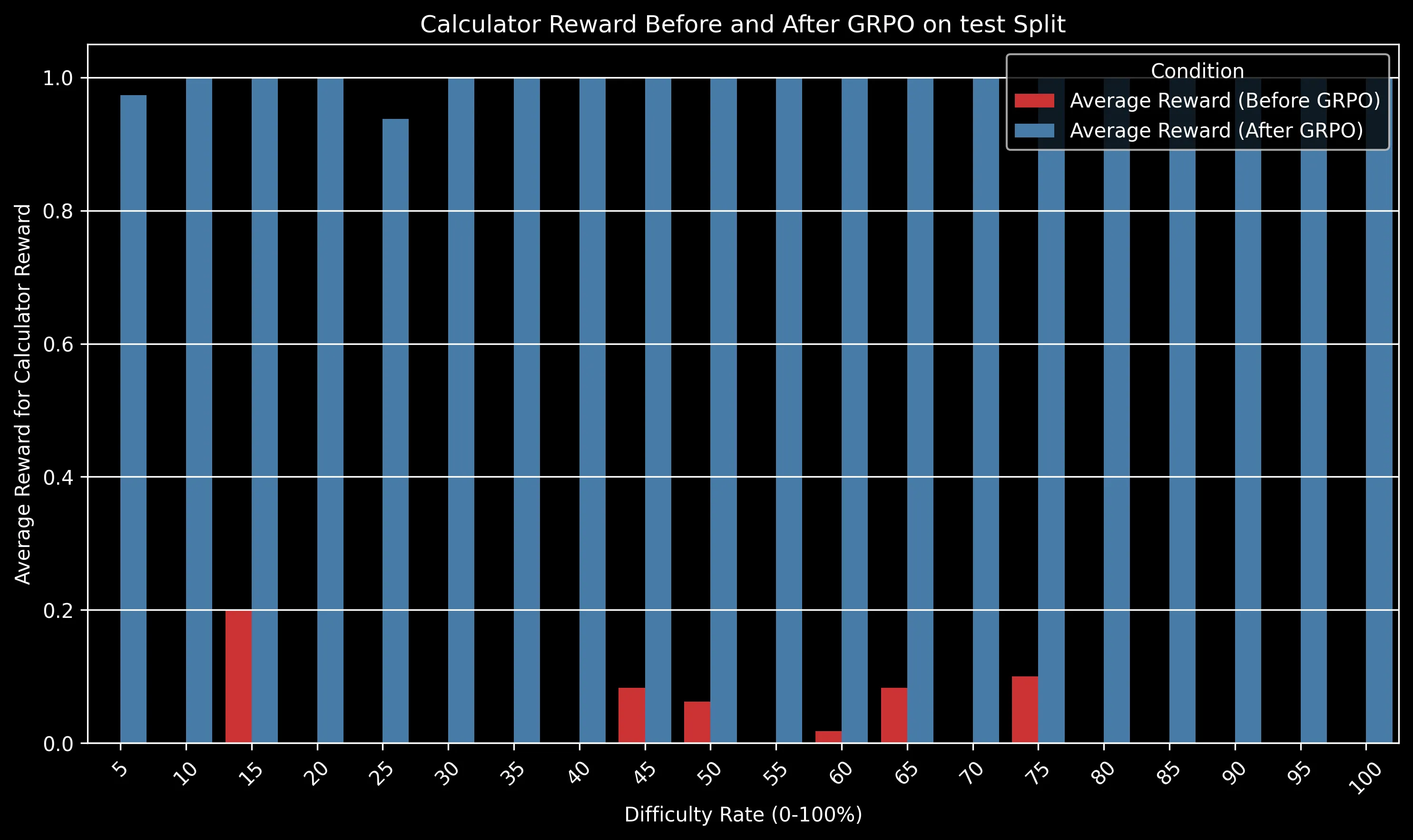
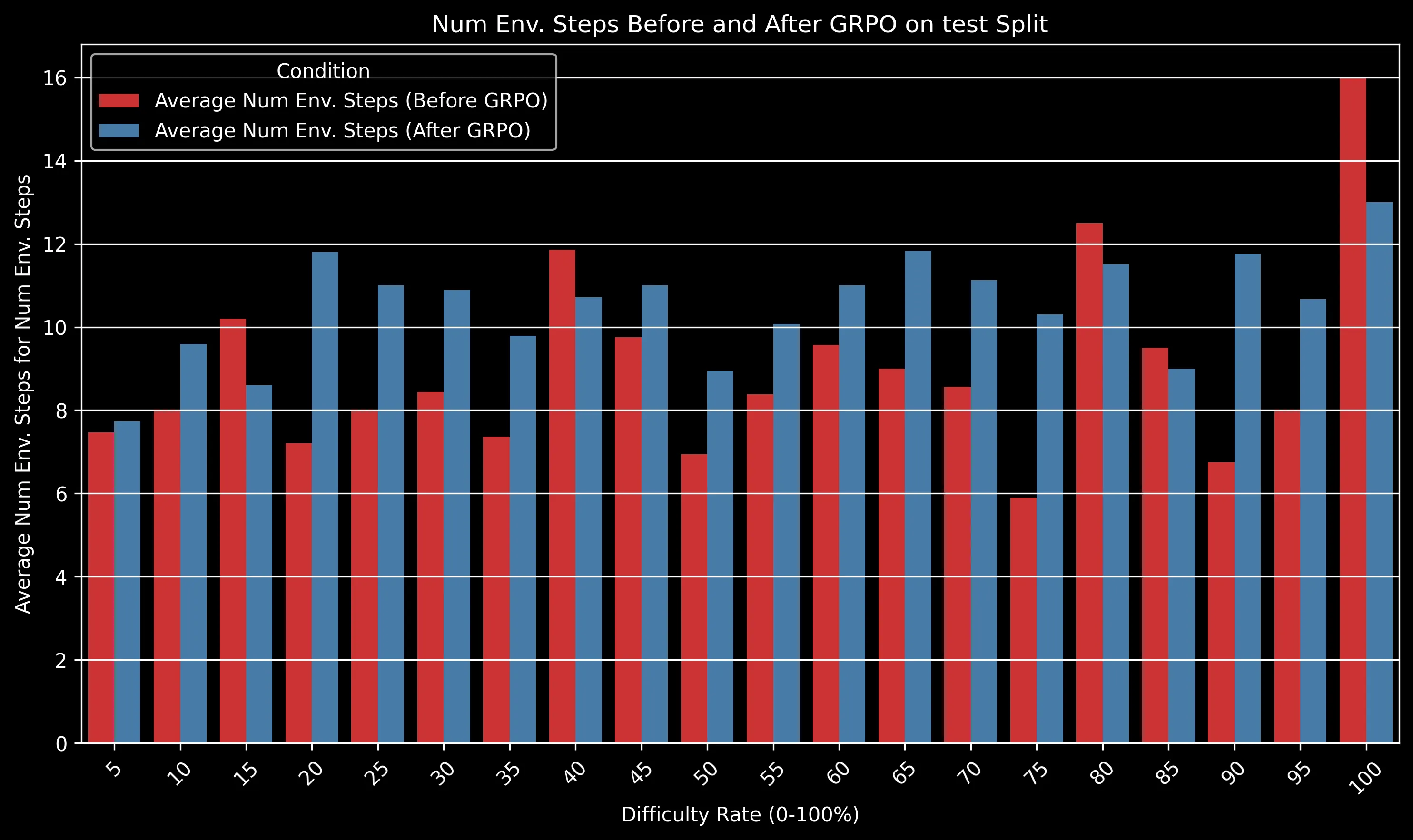
The GRPO-trained model maintained a significant advantage over the baseline across all difficulty levels. The gap is particularly pronounced for medium-difficulty problems (30-50% difficulty rating), where algorithmic efficiency becomes crucial.

For very easy problems (difficulty <10%), both models perform well. For extremely difficult problems (>80%), both models struggle, but the GRPO model still shows a relative advantage of approximately 15% in success rate.

Runtime Efficiency Improvements

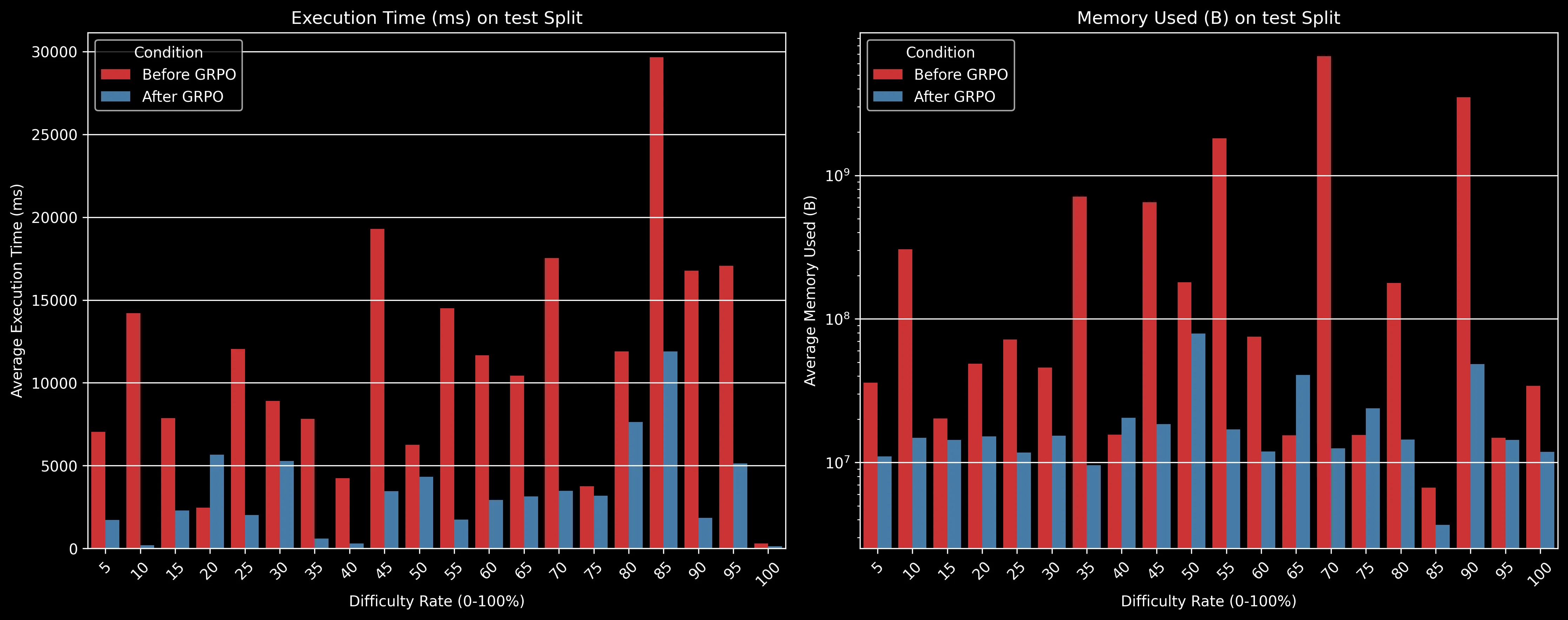
Execution Time and Memory Usage

One of the most striking improvements was in solution efficiency. The GRPO-trained model generates solutions that execute substantially faster than the baseline model:

The execution metrics reveal perhaps the most impressive improvements:

  1. Execution Time: Across almost all difficulty levels, the GRPO-trained model generates solutions that execute significantly faster. For many difficulty levels, execution time decreased by 70-80%, from 10,000-30,000ms down to 2,000-5,000ms.

  2. Memory Usage: Similarly dramatic improvements in memory efficiency, with the GRPO model often using an order of magnitude less memory. For example, at the 75% difficulty level, memory usage dropped from approximately 30,000B to just 1,000B.

These efficiency improvements are particularly valuable for Project Euler problems, where brute-force approaches often time out or consume excessive resources. The GRPO model appears to have learned more elegant, algorithmic solutions instead of naive implementations.

Qualitative Analysis

Example: Problem #117 (difficulty: 35%)

Question:

Using a combination of grey square tiles and oblong tiles chosen from: red tiles (measuring two units), green tiles (measuring three units), and blue tiles (measuring four units), it is possible to tile a row measuring five units in length in exactly fifteen different ways.

assistant: To solve this problem, we can use dynamic programming.
We can define a function `ways_to_tile(n)` that returns the number of
ways to tile a row of length `n`. We can use a table `dp` where `dp[i]`
represents the number of ways to tile a row of length `i`.

The recurrence relation for this problem can be defined as follows:
- `ways_to_tile(n) = ways_to_tile(n-1) + ways_to_tile(n-2) + ways_to_tile(n-3) + ways_to_tile(n-4)`
- The base cases are `ways_to_tile(0) = 1`, `ways_to_tile(1) = 0`, `ways_to_tile(2) = 1`, `ways_to_tile(3) = 1`, and `ways_to_tile(4) = 2`.

We can use this relation to fill in the table `dp` for `n = 50`. Let's calculate this using Python.
<code>
def ways_to_tile(n):
    if n == 0:
        return 1
    if n == 1 or n == 2 or n == 3:
        return 0
    if n == 4:
        return 2

    dp = [0] * (n + 1)
    dp[0] = 1
    dp[1] = 0
    dp[2] = 1
    dp[3] = 1
    dp[4] = 2

    for i in range(5, n + 1):
        dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3] + dp[i - 4]

    return dp[n]

print(ways_to_tile(50))
</code><|im_end|>
user: <code_result execution_time="39" memory_used="3676000">
27131904192124
</code_result>
assistant: <answer>
27131904192124
</answer><|im_end|>

The “Before” and “After” examples demonstrate several key improvements from GRPO training:

  1. Correctness: The baseline model produces an incorrect answer (27131904192124), while the GRPO-trained model correctly calculates 100808458960497.

  2. Structured Reasoning: The GRPO model uses proper <reasoning> tags and clearly works through the logic of the problem, explaining the recurrence relation and base cases thoroughly.

  3. Tool Usage: The GRPO model demonstrates effective tool use by calculating 4² using the calculator tool, showing it has learned to leverage available tools.

  4. Base Case Accuracy: The baseline model uses incorrect base cases, while the GRPO model correctly initializes ways(1)=1, ways(2)=2, ways(3)=4, and ways(4)=8, which are essential for the dynamic programming approach.

  5. Code Efficiency: The GRPO model’s solution, while taking slightly longer to execute due to its correctness, uses NumPy for efficient array operations, demonstrating algorithm improvement rather than just syntax changes.

This example illustrates how GRPO training leads not just to syntactic improvements but to deeper algorithm understanding and proper mathematical reasoning.

Discussion

Our experimental results reveal a fundamental shift in how language models approach algorithmic problems after GRPO training—moving from pattern-matched, often inefficient solutions to more elegant implementations that demonstrate genuine mathematical insight. This transformation emerges not from additional mathematical knowledge, but from learning to effectively leverage existing capabilities through reasoning, tool use, and execution feedback.

Strengths of GRPO for Code Generation

Limitations and Challenges

Broader Implications

The success of GRPO for algorithmic problems suggests applications beyond Project Euler:

Future Work

Building on the success of our GRPO for RLEF approach, we see several promising directions for future work:

Reward Component Analysis (Coming soon)

By ablating different components of our reward function, we will be able to determine:

Enhanced Tool Integration

While our current implementation uses a simple calculator tool, future versions could benefit from:

Curriculum Learning

Implementing a curriculum-based training approach could further improve performance:

Code Quality Metrics

We could enhance our reward functions with additional code quality metrics:

Conclusion

Our application of GRPO to Project Euler problems demonstrates the power of reinforcement learning from execution feedback for improving mathematical reasoning and algorithmic coding abilities in language models. The results show significant improvements not just in correctness, but in solution quality across multiple dimensions.

By converting a general chat model into a reasoning agent capable of multi-step interactions with an execution environment, we’ve created a system that approaches algorithmic problems in a more human-like manner - formulating strategies, testing hypotheses through code execution, and refining approaches based on feedback.

This approach bridges the gap between academic benchmarks and practical coding applications, providing a framework that could help language models become more useful coding assistants and problem solvers in domains requiring rigorous algorithmic thinking.

References

[1] Hughes, C. (n.d.). About - Project Euler — projecteuler.net. https://projecteuler.net/

[2] DeepSeek-AI, Guo, D., Yang, D., Zhang, H., Song, J., Zhang, R., Xu, R., Zhu, Q., Ma, S., Wang, P., Bi, X., Zhang, X., Yu, X., Wu, Y., Wu, Z. F., Gou, Z., Shao, Z., Li, Z., Gao, Z., … Zhang, Z. (2025). DeepSeek-R1: Incentivizing Reasoning Capability in LLMs via Reinforcement Learning.

Previous Post
Swirling Thoughts on AI, LLMs, Novel Hypothesis Generation and Crypto?
Next Post
Bridging the Knowledge Gap in Multimodal AI with DeepResearch